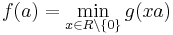Euclidean domain
In mathematics, more specifically in abstract algebra and ring theory, a Euclidean domain (also called a Euclidean ring) is a ring that can be endowed with a certain structure – namely a Euclidean function, to be described in detail below – which allows a suitable generalization of the Euclidean algorithm. This generalized Euclidean algorithm can be put to many of the same uses as Euclid's original algorithm in the ring of integers: in any Euclidean domain, one can apply the Euclidean algorithm to compute the greatest common divisor of any two elements. In particular, the greatest common divisor of any two elements exists and can be written as a linear combination of them (Bézout identity). Also every ideal in a Euclidean domain is principal, which implies a suitable generalization of the Fundamental Theorem of Arithmetic: every Euclidean domain is a unique factorization domain.
It is important to compare the class of Euclidean domains with the larger class of principal ideal domains (PIDs). An arbitrary PID has much the same "structural properties" of a Euclidean domain (or, indeed, even of the ring of integers), but knowing an explicit Euclidean function gives a concreteness which is useful for algorithmic applications. Especially, the fact that the integers and any polynomial ring in one variable over a field are Euclidean domains with respect to easily computable Euclidean functions is of basic importance in computational algebra.
So, given an integral domain R, it is often very useful to know that R has a Euclidean function: in particular, this implies that R is a PID. However, if there is no "obvious" Euclidean function, then determining whether R is a PID is generally a much easier problem than determining whether it is a Euclidean domain.
Euclidean domains appear in the following chain of class inclusions:
- Commutative rings ⊃ integral domains ⊃ integrally closed domains ⊃ unique factorization domains ⊃ principal ideal domains ⊃ Euclidean domains ⊃ fields
Contents |
Motivation
Consider the set of integers with the natural operations of + and ⋅. The familiar concept of long division on the integers relies heavily on the following fact: Given an integer a and a non-zero integer b, there exists integers q and r with a = q⋅b + r, and furthermore, with r = 0 or |r| < |b|. If we only were to have considered positive a and b, this restriction on r and b may be expressed as r = 0, or r < b. Any ring has a notion of addition and multiplication so it is conceivable to think that this notion of long division may be generalized to any ring. However, the requirement on the remainder and the quotient (r = 0 or r < b) cannot be easily defined in the context of rings, unless of course there exists an ordering of some sort defined on the ring. This leads to the concept of a Euclidean domain, where the ring is equipped with a norm, called its "degree function", mapping each element in the ring to its distance from the additive identity 0. So rather than requiring r = 0 or r < b, we may lift this to r = 0 or d(r) < d(b). The essential idea behind a Euclidean domain is a ring, any element of which (a) and any non-zero element of which (b) have the property that there exists a multiple of b not too far away from a. Of course, if the ring happens to be a division ring (or a field), a⋅b−1 yields a multiple of b (the pre-multiplication of this entity with b), which gives a. So for fields and division rings, there exists a multiple of b which exactly matches with a. Of course this need not be true in general (e.g. it fails for the integers) so the restriction is relaxed to just "a multiple of b sufficiently close to a". The natural question to ask is what the range of the degree function is defined to be. For many purposes, and in particular for the purpose that the Euclidean algorithm should hold, the range is defined to be the natural numbers. The crucial property of the natural numbers, here, is that they are well-ordered.
Definition
Let R be an integral domain. A Euclidean function on R is a function 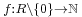 satisfying the following fundamental division-with-remainder property:
satisfying the following fundamental division-with-remainder property:
- (EF1) If a and b are in R and b is nonzero, then there are q and r in R such that a = bq + r and either r = 0 or f(r) < f(b).
A Euclidean domain is an integral domain which can be endowed with at least one Euclidean function. It is important to note that a particular Euclidean function f is not part of the structure of a Euclidean domain: in general, a Euclidean domain will admit many different Euclidean functions.
Most algebra texts require a Euclidean function to have the following additional property:
- (EF2) For all nonzero a and b in R, f(a) ≤ f(ab).
However, one can show that (EF2) is superfluous in the following sense: any domain R which can be endowed with a function g satisfying (EF1) can also be endowed with a function f satisfying (EF1) and (EF2): indeed, for 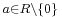 one can define f(a) as follows. (Rogers 1971)
one can define f(a) as follows. (Rogers 1971)
In words, one may define f(a) to be the minimum value attained by g on the set of all non-zero elements of the principal ideal generated by a.
Notes on the definition
Many authors use other terms such as "degree function", "valuation function", "gauge function" or "norm function", in place of "Euclidean function". Some authors also require the domain of the Euclidean function be the entire ring R; this can always be accommodated by adding 1 to the values at all nonzero elements, and defining the function to be 0 at the zero element of R, but the result is somewhat awkward in the case of K[X]. The definition is sometimes generalized by allowing the Euclidean function to take its values in any well-ordered set; this weakening does not affect the most important implications of the Euclidean property.
The property (EF1) can be restated as follows: for any principal ideal I of R with nonzero generator b, all nonzero classes of the quotient ring R/I have a representative r with f(r) < f(b). Since the possible values of f are well-ordered, this property can be established by proving f(r) < f(b) for any r (not in I) with minimal value of f(r) in its class. Note that for a Euclidean function that is so established there need not exist an effective method to determine q and r in (EF1).
Examples
Examples of Euclidean domains include:
- Any field. Define f(x) = 1 for all nonzero x.
- Z, the ring of integers. Define f(n) = |n|, the absolute value of n.[1]
- Z[i], the ring of Gaussian integers. Define f(a + bi) = a2 + b2, the squared norm of the Gaussian integer a + bi.
- Z[ω] (where ω is a cube root of 1), the ring of Eisenstein integers. Define f(a + bω) = a2 − ab + b2, the norm of the Eisenstein integer a + bω.
- K[X], the ring of polynomials over a field K. For each nonzero polynomial P, define f(P) to be the degree of P.[2]
- K[[X]], the ring of formal power series over the field K. For each nonzero power series P, define f(P) as the degree of the smallest power of X occurring in P. In particular, for two nonzero power series P and Q, f(P)≤f(Q) iff P divides Q.
- Any discrete valuation ring. Define f(x) to be the highest power of the maximal ideal M containing x (equivalently, to the power of the generator of the maximal ideal that x is associated to). The previous case K[[X]] is a special case of this.
- A Dedekind domain with finitely many nonzero prime ideals P1, ..., Pn. Define
 , where
, where 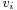 is the discrete valuation corresponding to the ideal Pi. (Samuel 1971)
is the discrete valuation corresponding to the ideal Pi. (Samuel 1971)
Properties
Let R be a domain and f a Euclidean function on R. Then:
- R is a principal ideal domain. In fact, if I is a nonzero ideal of R then any element a of I\{0} with minimal value (on that set) of f(a) is a generator of I.[3] As a consequence R is also a unique factorization domain and a Noetherian ring. With respect to general principal ideal domains, the existence of factorizations (i.e., that R is an atomic domain) is particularly easy to prove in Euclidean domains: choosing a Euclidean function f satisfying (EF2), x cannot have any decomposition into more than f(x) nonunit factors, so starting with x and repeatedly decomposing reducible factors is bound to produce a factorization into irreducible elements.
- Any element of R at which f takes its globally minimal value is invertible in R. If an f satisfying (EF2) is chosen, then the converse also holds, and f takes its minimal value exactly at the invertible elements of R.
- If the Euclidean property is algorithmic, i.e., if there is a division algorithm that for given a and nonzero b produces a quotient q and remainder r with a = bq + r and either r = 0 or f(r) < f(b), then an extended Euclidean algorithm can be defined in terms of this division operation.[4]
Not every PID is Euclidean. For example, for d = −19, −43, −67, −163, the ring of integers of 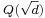 is a PID which is not Euclidean, but the cases d = −1, −2, −3, −7, −11 are Euclidean.[5]
is a PID which is not Euclidean, but the cases d = −1, −2, −3, −7, −11 are Euclidean.[5]
However, in many finite extensions of Q with trivial class group, the ring of integers is Euclidean (not necessarily with respect to the absolute value of the field norm; see below). Assuming the extended Riemann hypothesis, if K is a finite extension of Q and the ring of integers of K is a PID with an infinite number of units, then the ring of integers is Euclidean.[6] In particular this applies to the case of totally real quadratic number fields with trivial class group. In addition (and without assuming ERH), if the field K is a Galois extension of Q, has trivial class group and unit rank strictly greater than three, then the ring of integers is Euclidean.[7] An immediate corollary of this is that if the number field is Galois over Q, its class group is trivial and the extension has degree greater than 8 then the ring of integers is necessarily Euclidean.
Norm-Euclidean fields
Algebraic number fields K come with a canonical norm function on them: the absolute value of the field norm N that takes an algebraic element α to the product of all the conjugates of α. This norm maps the ring of integers of a number field K, say OK, to the nonnegative rational integers, so it is a candidate to be a Euclidean norm on this ring. If this norm satisfies the axioms of a Euclidean function then the number field K is called norm-Euclidean. Strictly speaking it is the ring of integers that is Euclidean since fields are trivially Euclidean domains, but the terminology is standard.
If a field is not norm-Euclidean then that does not mean the ring of integers is not Euclidean, just that the field norm does not satisfy the axioms of a Euclidean function. Indeed, there are examples of number fields whose ring of integers is Euclidean but not norm-Euclidean, a simple example being the quadratic field 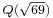 . Finding all such fields is a major open problem, particularly in the quadratic case.
. Finding all such fields is a major open problem, particularly in the quadratic case.
The norm-Euclidean quadratic fields have been fully classified, they are 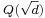 where d takes the values
where d takes the values
- −11, −7, −3, −2, −1, 2, 3, 5, 6, 7, 11, 13, 17, 19, 21, 29, 33, 37, 41, 57, 73 (sequence A048981 in OEIS).
Notes
Rogers, Kenneth (1971), "The Axioms for Euclidean Domains", American Mathematical Monthly (The American Mathematical Monthly, Vol. 78, No. 10) 78 (10): 1127–1128, doi:10.2307/2316324, JSTOR 2316324
- ^ Fraleigh & Katz (1967), p. 377, Example 1
- ^ Fraleigh & Katz (1967), p. 377, Example 2
- ^ Fraleigh & Katz (1967), p. 377, Theorem 7.4
- ^ Fraleigh & Katz (1967), p. 380, Theorem 7.7
- ^ Motzkin, Theodore (1949), "The Euclidean algorithm", Bulletin of the American Mathematical Society 55 (12): 1142–1146, doi:10.1090/S0002-9904-1949-09344-8, http://projecteuclid.org/handle/euclid.bams/1183514381
- ^ Weinberger, Peter J. (1973), "On Euclidean rings of algebraic integers", Proceedings of Symposia in Pure Mathematics (AMS) 24: 321–332
- ^ Harper, Malcolm; Murty, M. Ram (2004), "Euclidean rings of algebraic integers", Canadian Journal of Mathematics 56 (1): 71–76, doi:10.4153/CJM-2004-004-5, http://www.mast.queensu.ca/~murty/harper-murty.pdf
References
- John B. Fraleigh, Victor J. Katz. A first course in abstract algebra. Addison-Wesley Publishing Company. 5 ed., 1967. ISBN 0-201-53467-3
- Pierre Samuel, "About Euclidean rings", Journal of Algebra 19 (1971) 282-301.